What's in your panel? Many homebuilts and LSA's today have instrumentation that rivals what CAFE used for their excellent APR* reports of only a few years ago.
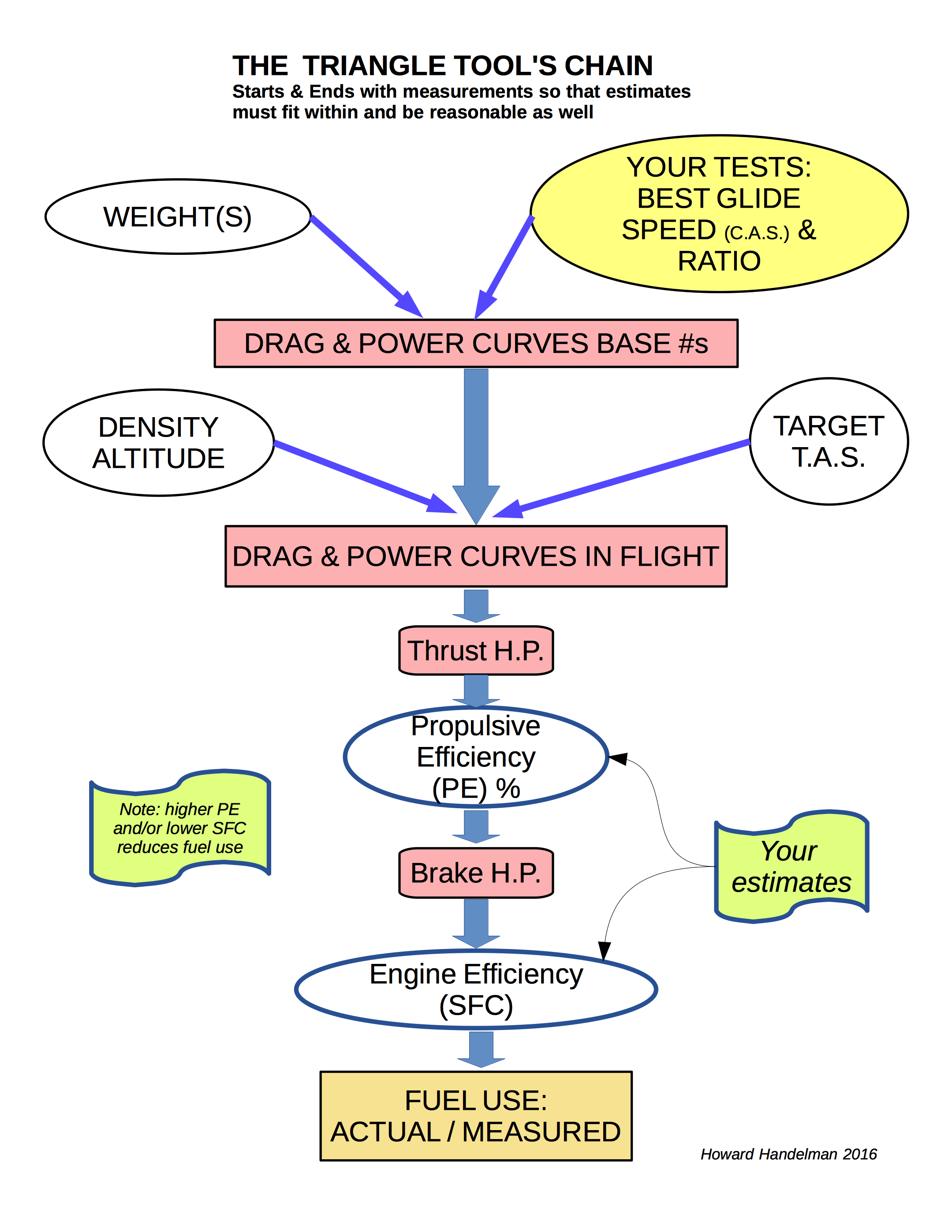
Discover the chain of calculations that begins with weight and span and ends with fuel burn rate for which everything between must fit. Do some easy, fun test flying. Then find your best range or your Carson speed** or make smart choices about altitude and airspeed to fly. With this tool and the included self-testing instructions you can do it all without math. The built-in formulas are standard; this package ties them together in a new way.
Every year at AirVenture there are new airplanes that predict excellent performance. Some of them claim numbers that are improbable. You may also find that most propellers don't deliver the efficiency claimed. This tool lets you check because all the chain links must fit.
“We can lift ourselves out of ignorance, we can find ourselves as creatures of excellence and intelligence and skill.”
― Richard Bach, Jonathan Livingston Seagull
* http://cafe.foundation/v2/research_aprs.php
** Carson speed is a theoretical optimum speed or the best compromise between speed and economy. http://cafe.foundation/v2/pdf_tech/MPG.engines/AIAA.1980.1847.B.H.Carson.pdf
Introduction
The Triangle Tool uses your data. The only static data are Span, Area & Glide Ratio. Since the others can change, the tool uses data that apply as a set to a specific time slice of flight. The Tool provides sub-tools for converting to CAS and more. It also has a sheet for making method 2 easy to use. The inputs are:
-
Physical and measured or specified: (static) Weight, (static) Wing Span, (static) Wing Area
-
Measured per time slice: Target Speed (TAS), Density Altitude, Fuel Consumption
-
Measured or Computed: (static) Glide Ratio (L/D max), Speed for L/D max (CAS, weight and atmosphere dependent),
-
Estimated or Derived: SFC (varies with design, condition, load, RPM and mixture), Propulsive Efficiency (PE) (net and varies)
This describes proposed methods for finding and/or estimating the last four items above as applicable to a given speed, altitude and fuel consumption. In the best case, if you are successful with these methods, the Tool will tell you the PE with equal accuracy.
Method 1: Fuel Flow and SFC
The purpose of this method is to find the fuel flow for a given set of flight data with a reasonably accurate estimate for SFC. Thus you will use the engine at its most accurately knowable SFC. Once these two variables are known to a reasonable degree of accuracy, the remaining unknown (after completing method 2) will be Propulsive Efficiency (PE) alone; the Tool will compute it for you.
The tool's chain of data and calculations ends with fuel consumption at a given flight's set of air and performance data. Using the tool, you can increment any unknowns to get to one solution, or several very similar ones reaching the right result (fuel flow) observed for a given flight condition.
A medium cruise speed is a good place to start, but top speed and economy cruise are useful as well. Since PE will vary, they are all potentially useful.
-
Fly at 8000' or higher density altitude. Record pressure altitude, indicated altitude, GPS altitude and OAT. This altitude provides smooth air and keeps power percent safe. GPS altitude is usually slightly different than true altitude but is a useful validity check.
-
Optionally set instruments to read in km/h for better accuracy. If you do you, may need to work with altitude in meters or have a second instrument that reads in feet.
-
Fly level at a predetermined speed: IAS, TAS, CAS. Note wind and adjust heading to minimize GS vs TAS. Record all 3 speeds for later.
-
Adjust mixture to best power and resume target speed and altitude. This can also be done usefully at LOP but the SFC at best power is the most accurately knowable and best power is the most able to be found/set accurately. Why not do both? Best power can be found pretty accurately either by ear and/or by the simple measurement of IAS at a constant altitude and constant throttle, varying only mixture. For most engines used in GA, the SFC at best power is easily found in manufacturer data. For example, most Lycoming type engines at non-extreme compression ratios will have a best power SFC of .48~.52 pounds per HP per hour. You will enter that estimated factor in the Tool. Engines with electronic ignition can have a lower SFC but usually that is more noticeable at LOP than at best power. An example of manufacturer data is appended.
Tip: this kind of testing is much easier with an auto-pilot that can hold both heading and altitude!
-
Observe and record all data but especially RPM and fuel flow. Record fuel onboard for later weight calculation. Record MPG, etc. if you can, as a cross-check.
Just for curiosity, record deck angle! This will allow you to calculate AOA later. That has nothing to do with the tool except that the tool will calculate the coefficient of lift at best AOA.
Method 2: Speed for Best Glide (V l/d max) & Best Glide Ratio (BGR)
The purpose of this method is to find the speed for V l/d max and possibly the sink rate at that speed. That in turn allows the computation of BGR. It is weight sensitive. A few methods are given, some of which also give sink rate.
Note: In 1995 Jack Norris and Andy Bauer with CAFE made a C-152 into a glider to repeat and improve on work done by Raspet years earlier. Jack later developed the Zero Thrust Device to detect when the prop is providing neither pull nor push-back and discovered for his Luscombe that there is a revolutions per mile at which this occurs and it's a constant for a given airplane. That's still the best method but these methods are suggested as useful alternatives. See Sport Aviation and other published articles.
Tip: The sink rate at V l/d max is greater than minimum sink. The Tool provides an entry field for best BGR and the CAS for it, given a known weight. By using several tests, the data can be cross-checked. If you can determine both V l/d max and sink rate then you will have better answers from the Tool.
Tip: A good way to detect glide ratio is by using the glide ratio field on any Garmin handheld GPS, which may need to be configured by the user. Beware: the GPS is showing/calculating sink vs ground speed so it is wind sensitive and the most accuracy results from either zero wind or zero HW/TW component.
-
Fly level at lowest possible power. Try multiple altitudes and if you have a CS prop, I suggest forcing the prop to fully fine pitch simply because that is most likely to be accurately repeatable at low speed. Record fuel on board for weight. The actual power doesn't matter but the speed for minimum power is what you want to know. Convert observed speed to CAS. For reasons too difficult for this document, this speed may be a little different than the “true” speed for minimum sink.
-
Using the best guess for zero thrust rev's per mile (ZTR/M), glide at the best glide ratio you can find via GPS and record speed, sink, weight factors. CAS.The GPS will give you a more accurate sink rate than your atmospheric instruments. Caution for wind affecting GPS based data. The best guess for ZTR/M can be determined by a different tool which is given elsewhere. It is based on the physical pitch of the prop and the “slip”. If feasible, “bracket” the observations.
-
Starting with best guess for ZTR/M, use slightly more revs but well below power required for level flight and find V l/d max as indicated on the GPS. As before, the CAS is what is needed but the guess will be at a TAS value. This is not easy. You will later convert from TAS to CAS. The actual glide ratio or L/D is not meaningful in this test, only the speed. Because you are using partial power, the indicated glide ratio will be better (higher) than the “true” value.
-
Use about the same very low power as in #3 and find the speed for minimum sink (It will be lower than for V l/d max). It will be close to the result in #1
-
Use the same ZTR/M (but not the same actual rev's) as in #2 and find the speed for minimum sink and the rate of sink. This is lower power than used in #3 and #4. This speed's sink rate will be lower than the one from #4 but the speed should be about the same.
Clarification: V minimum sink is ((V L/D max)/1.316074). Power is speed times drag. Even though the drag is higher at the lower speed, the speed is lower so the multiplied result is lower. The power at V L/D max will be 1.1398 times V minimum power (or +14%). Power also equals weight x sink_rate. Since weight is equal, the sink difference will be in proportion to the power difference 1.1398 or +14%. Stated simply, the speed for minimum sink takes least power (by definition!) and the speed for L/D max takes 14% more power than for minimum sink (usually also equal to maximum endurance, btw).
You now have several test result speeds for BGR either directly observed or derived from observed minimum sink. The one from level flight may be a little higher and the others will likely (should) be very close. I like using the lower speed value(s) for reasons discussed elsewhere. There should also be differences due to weight, of course. If the second and third, etc. are quite close then the sink rates should be useable as well.
Use the “Testing Methods Aid” sheet in the Tool to do the math and show the relationships clearly.
Method 3: Climb on the Curve |
From the above methods we have a picture of the airplane's drag and power required. Now we can test and confirm and learn a bit more about the PE.
An example using an RV will make this clearer: Fly the airplane level at a speed a little greater than the theoretical Carson speed. For reasons that will be clearer later, use a mixture that's A] full rich or B] best power or C] 50 or 75 degrees LOP. Record the TAS, pressure altitude, OAT, fuel flow, RPM and everything else you can observe. Let's assume in this example the fuel flow is 7 gph. Now increase the fuel flow by 1 gph at the chosen mixture which may need to be adjusted to keep it the same. Hold the indicated airspeed constant. You will climb, so the TAS will probably change. The eventual airspeed that matters will be CAS. Now observe and record the rate of climb. This assumes you know the weight. The triangle in the tool says you know the THP being used to climb (rate of climb times weight, etc.). What have you just learned?
We learned that a given THP change will make the aircraft climb at a given rate. We think we know the THP from which we started because we think we know the point on the drag curve where we started. We held CAS constant so the increased fuel flow of 1 gph produced net power of (weight x climb). 1 gph is 6 pounds per hour. If the SFC is closely estimated (.40 in this example) then the BHP change would be (6 / .4 = 15 BHP. If the THP comes out 10 in the example then if the SFC is right, the PE is 67% (10/15). Get it? This can help validate your data. Your SFC won't be perfect but if you use a known, repeatable seting like full rich or LOP it will be close. If a 1500 pound RV holds its airspeed and begins to climb 250 feet per minute then we are using an additional (1500 x 250 = 375,000 foot pounds of energy) Since 1 HP is 33,000 foot pounds, we are actually using 375,000/33,000 = 11.4 HP. That is THP in this example. That would mean that .40 SFC and 76% PE would be correct in combination. The numbers move in opposite directions. A greater SFC, say 50%, would produce less power on the same fuel consumption (12 HP) so the PE would have to be higher: 95% in this example and quite likely not a correct answer.
Now let's go back to the 7gph starting point and use the same PE and the same SFC. Does that match the results from the first two methods? If not, then how big is the error?
A final note on this method: It ought to work just as well by decreasing the fuel flow and measuring the sink. Using it both ways would be worthwhile, then. Since propeller efficiency and even SFC will vary with changed rpm, fuel flow and altitude, it would be logical to use the smallest change in fuel flow that would produce an easily measured change in climb or sink from zero/level. I used 1 gph as an example.